Abstract
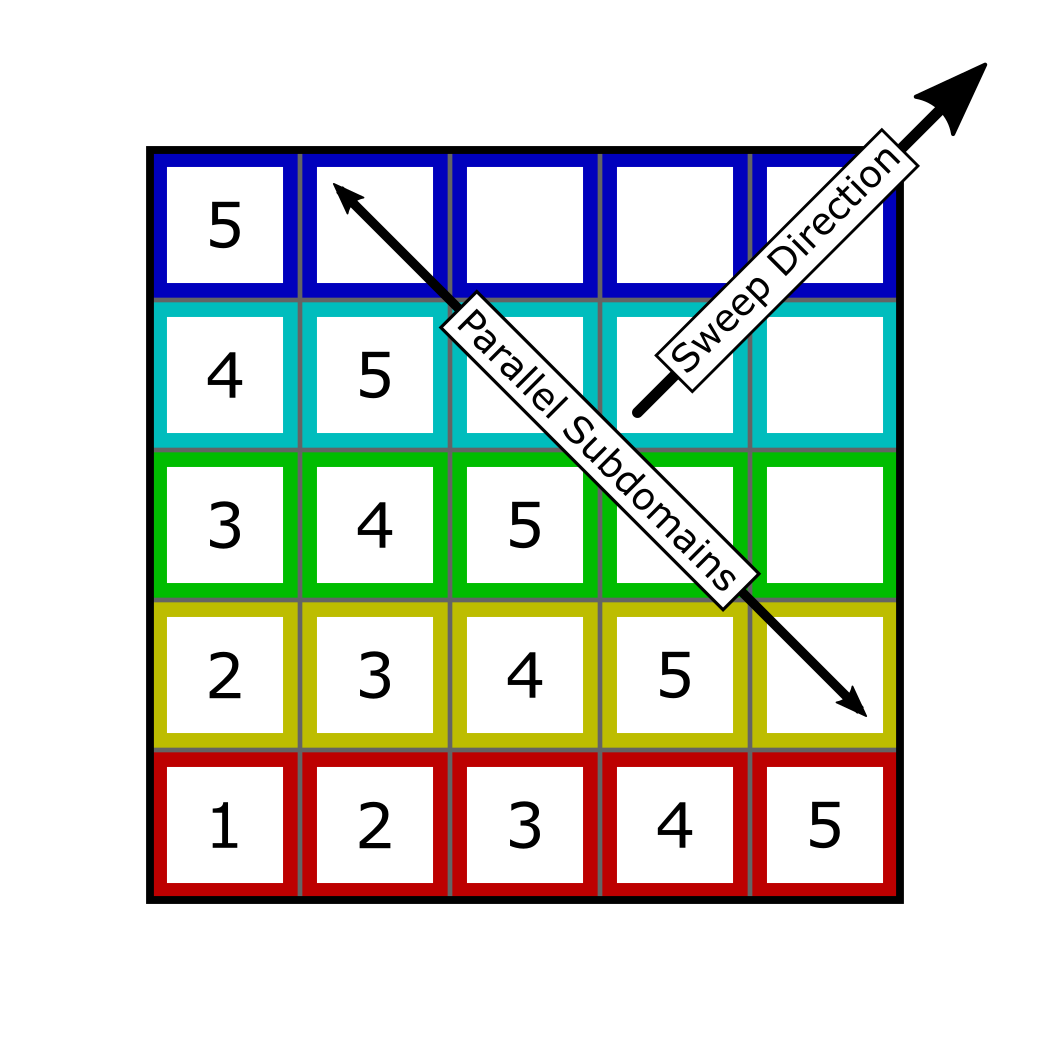
We present the first fast solver for the high-frequency Helmholtz equation that scales optimally in parallel, for a single right-hand side. The L-sweeps approach achieves this scalability by departing from the usual propagation pattern, in which information flows in a 180 degree cone from interfaces in a layered decomposition. Instead, with L-sweeps, information propagates in 90 degree cones induced by a checkerboard domain decomposition (CDD). We extend the notion of accurate transmission conditions to CDDs and introduce a new sweeping strategy to efficiently track the wave fronts as they propagate through the CDD. The new approach decouples the subdomains at each wave front, so that they can be processed in parallel, resulting in better parallel scalability than previously demonstrated in the literature. The method has an overall O((N/p) log w) empirical run-time for N=n^d total degrees-of-freedom in a d-dimensional problem, frequency w, and p=O(n) processors. We introduce the algorithm and provide a complexity analysis for our parallel implementation of the solver. We corroborate all claims in several two- and three-dimensional numerical examples involving constant, smooth, and discontinuous wave speeds.
