Abstract
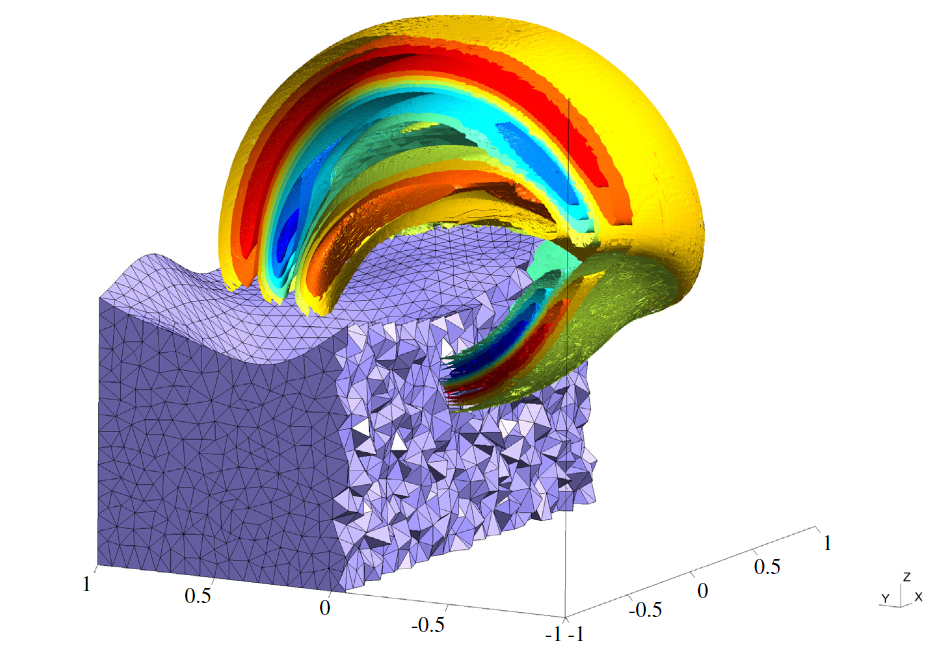
We present a high order time-domain nodal discontinuous Galerkin method for wave problems on hybrid meshes consisting of both wedge and tetrahedral elements. We allow for vertically mapped wedges which can be deformed along the extruded coordinate, and present a simple method for producing quasi-uniform wedge meshes for layered domains. We show that standard mass lumping techniques result in a loss of energy stability on meshes of vertically mapped wedges, and propose an alternative which is both energy stable and efficient. High order convergence is demonstrated, and comparisons are made with existing low-storage methods on wedges. Finally, the computational performance of the method on Graphics Processing Units is evaluated.
