Weight-adjusted discontinuous Galerkin methods: curvilinear meshes

Abstract

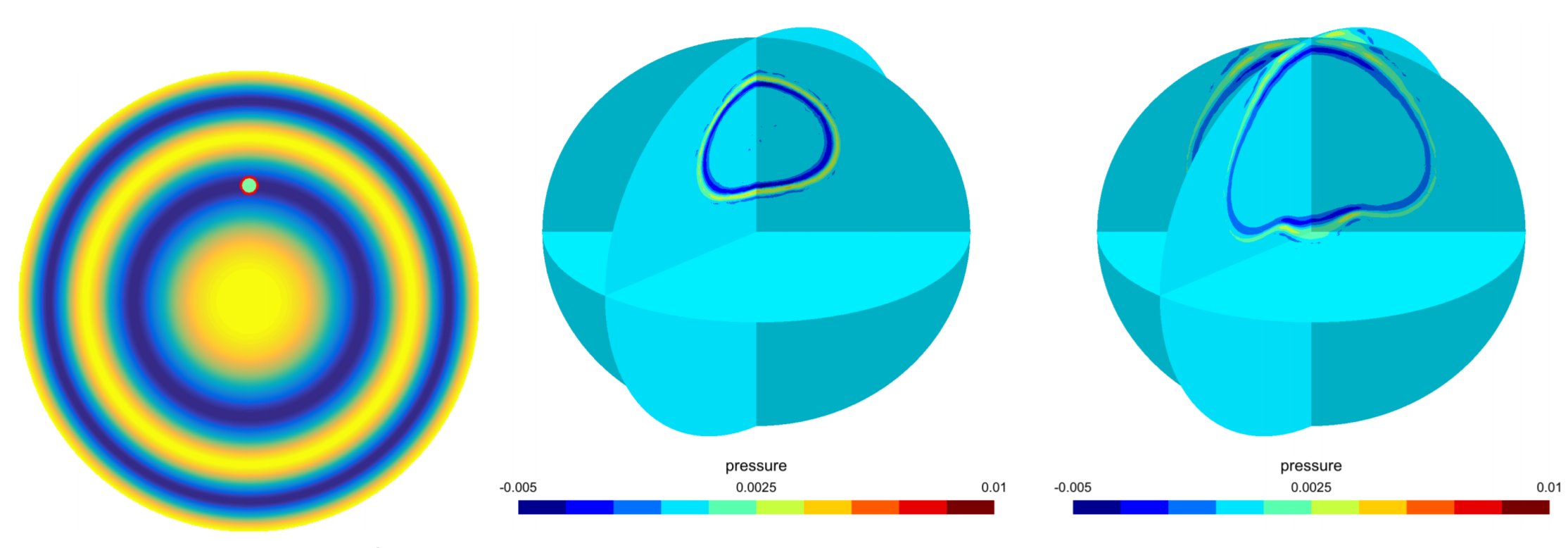
Traditional time-domain discontinuous Galerkin (DG) methods result in large storage costs at high orders of approximation due to the storage of dense elemental matrices. In this companion paper to Weight-adjusted discontinuous Galerkin methods: wave propagation in heterogeneous media, we propose weight-adjusted DG (WADG) methods for curvilinear meshes which reduce storage costs while retaining energy stability. A priori error estimates show that high order accuracy is preserved under sufficient conditions on the mesh, which are illustrated through convergence tests with different sequences of meshes. Numerical and computational experiments verify the accuracy and performance of WADG for a model problem on curved domains.